Dos matemáticos prueban unicidad para soluciones de la ecuación de Klein-Gordon
Fuente: Universidad de Sevilla
El Catedrático del Departamento de Análisis Matemático Alfonso Montes ha sido galardonado con el Premio Universidad de Sevilla a Trabajos de Investigación de Especial Relevancia en el Área de Ciencias por su trabajo en colaboración con Hakan Hedenmalm del Royal Institute of Technology of Stockholm Heisenberg uniqueness pairs and the Klein-Gordon equation. Este artículo científico se publicó en Annals of Mathematics en 2011, la revista quizás junto a Acta Mathematica más prestigiosa de esta área del conocimiento, y en el mismo se prueba que la solución de la ecuación de Klein-Gordon queda unívocamente determinada cuando se prescriben los valores sobre ciertos puntos bien localizados.
La ecuación de Klein-Gordon, llamada así en honor a los Físicos Oskar Klein y Walter Gordon, quienes en 1926 propusieron que la misma describe los electrones relativistas. Actualmente, es conocido que dicha ecuación es la ecuación del movimiento de los bosones sin espín, como es el caso del bosón de Higgs cuya existencia, aunque conjeturada en los años 60, tan sólo ha sido posible confirmarla este mismo año 2013. Montes y Hedenmalm también ponen en conexión su trabajo con el principio de incertidumbre de Heisenberg.
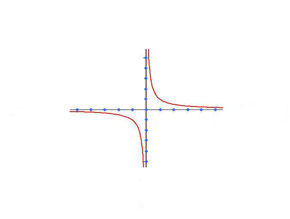
“Gracias a este nuevo avance matemático podemos conocer la información completa de una función a partir de una pequeña muestra o selección de datos siempre que la separación entre los puntos sea igual o inferior a 1, si por el contrario los valores son mayores que 1 entonces seguimos teniendo infinitas soluciones”, explica este investigador. En concreto, la ecuación de Klein-Gordon tiene asociada una hipérbola. Entonces basta conocer los valores de la función (definida en todo el plano) sobre los puntos señalados en azul en los ejes horizontal y vertical y siempre que la distancia entre los puntos del eje horizontal sea menor o igual a 1, para que la función, solución de la ecuación de Klein-Gordon, quede completamente determinada. En la figura de abajo se muestra el caso extremo en que la distancia entre los puntos es 1.
El grupo de investigación del profesor Montes sigue trabajando en esta línea y otras relacionadas, ya que han surgido “numerosos e interesantes problemas” relacionados con las soluciones de la ecuación de Klein-Gordon, algunos de ellos de Teoría de Números que permanecen abiertos desde los años 40´y aún se está estudiando cómo solucionarlos.
Fuente: Vicerrectorado de Investigación
Mª Carmen Escámez Almazo
comunicacioninves@us.es
Tfno.: 954550123
Móvil: 68201443
Últimas publicaciones
La Fundación Descubre-Consejería de Universidad, Investigación e Innovación y la Universidad Pablo de Olavide coordinan esta entidad regional que persigue la atención y asesoramiento a las iniciativas basadas en la participación activa de la ciudadanía. En su nueva convocatoria de ayudas, financiará 8 proyectos que aborden retos científicos y sociales de la región hasta junio de 2027.
El proyecto está financiado por el programa Erasmus+ de la Unión Europea y cuenta con la participación de instituciones de Italia, España y Francia.
Sigue leyendo
Un equipo de investigación de la Universidad de Cádiz ha creado un sistema basado en aprendizaje profundo capaz de localizar y clasificar automáticamente anomalías en radiografías de tórax. Los resultados mejoran la precisión de otros métodos utilizados y lo validan como una herramienta con potencial para dar soporte a la evaluación precoz de patologías del pulmón.
